Linear Programming In Python

Content

• Using Python And Julia To Solve Linear Programming Problems
• See How To Solve A Staffing Problem With Pulp, A Linear Programming Toolkit For Python
• Big Data Partner Resources
• Solving Linear Programming Problem With Python
• Duality

To improve the efficiency of the Simplex algorithm, George Dantzig and W. CPLEX uses the Revised Simplex algorithm, with a number of improvements. The CPLEX Optimizers are particularly efficient and can solve very large problems rapidly. You can tune some CPLEX Optimizer parameters to change the algorithmic behavior according to your needs. The fact that a variable is unbounded does not necessarily influence the solvability of the model and should not be confused with a model being unbounded. A model is unbounded when its objective value can be increased or decreased without limit. Last, modify the objective expression to add the penalization term.

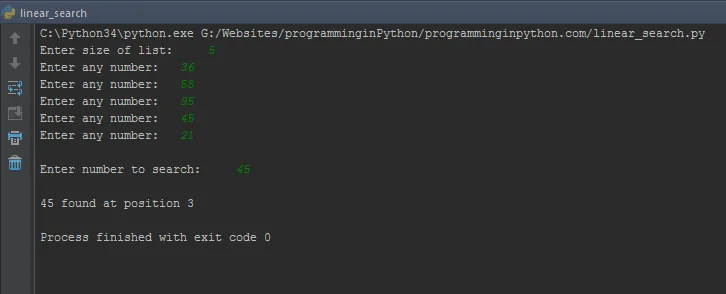
Variable x will contain the result vector and ret the return status of the call. May I suggest a solution that neither requires Pyomo nor Pulp? You can solve those systems by using the Fourier-Motzkin Method.

Using Python And Julia To Solve Linear Programming Problems

They allow you to solve a lot of current problems, for example, in planning project management, economic tasks, creating strategic planning. Method interior-point uses the primal-dual path following algorithm as outlined in .

$$ sum $$where a_i represents constants and x_i represents variables or unknowns. On Linux and OSX systems the tests must be run to make the default solver executable.

See How To Solve A Staffing Problem With Pulp, A Linear Programming Toolkit For Python

The value of the objective function is retrieved via the API call ‘get_objective’ and the values of the variables are retrieved via the API call ‘get_variables’. At last, the model is removed from memory via a call to ‘delete_lp’. Don’t forget this to free all memory allocated by lp_solve.

In the figure below it is possible to see the whole program for each language side by side, the Python script is on the left and the Julia script is on the right. If the inputs are put correctly in this structure, the method can be used, otherwise, it is necessary to make some changes in our modeling to adapt the problem to the acceptable structure. Because the left hand side of can never be positive, any assignment of values will satisfy the constraint. The presolve time was only 1.32 seconds and reduced the solution time from nearly half an hour to under 25 seconds. A reduction in problem size typically translates to a reduction in total run time. Modern LP solvers, such as CPLEX Simplex Optimizer, have built-in mechanisms to help escape such cycling by using perturbation techniques involving the variable bounds. # get slack value for painting time constraint, expected value is 0.

On the other hand, criss-cross pivot methods do not preserve feasibility – they may visit primal feasible, dual feasible or primal-and-dual infeasible bases in any order. Pivot methods of this type have been studied since the 1970s. Essentially, these methods attempt to find the shortest pivot path on the arrangement polytope under the linear programming problem. Dantzig’s original example was to find the best assignment of 70 people to 70 jobs. The computing power required to test all the permutations to select the best assignment is vast; the number of possible configurations exceeds the number of particles in the observable universe. However, it takes only a moment to find the optimum solution by posing the problem as a linear program and applying the simplex algorithm. The theory behind linear programming drastically reduces the number of possible solutions that must be checked.

It has been proven that the minima and maxima of linear programming problems lie at the vertices of the feasible region. In this example, there are only 4 corners to our feasible region, so we can find the solutions for each corner to find our maximum. In this set of notebooks we will be looking at some linear programming problems and how we can construct and solve these problems using the python linear programming package PuLP. The following diagram illustrates how the simplex algorithm traverses the boundary of the feasible region for the telephone production problem. The algorithm, starts somewhere along the edge of the shaded feasible region, and advances vertex-by-vertex until arriving at the vertex that also intersects the optimal objective line. Assume it starts at the red dot indicated on the diagam. In this topic, you’ll analyze a simple production problem in terms of decision variables, the objective function, and constraints.

Big Data Partner Resources

This will list the objective function, the decision variables and the constraints imposed on the problem. A linear programming problem is unbounded if its feasible region isn’t bounded and the solution is not finite. This means that at least one of your variables isn’t constrained and can reach to positive or negative infinity, making the objective infinite as well. This work presents an integer linear programming formulation for solving the MPR problem when considering duplications, losses, and coalescence, and shows that the new algorithm is both accurate and scalable. This paper introduces the PuLP library, an open source package that allows mathematical programs to be described in the Python computer programming language.

As for Python, while there are some pure-Python libraries, most people use a native library with Python bindings. There is a wide variety of free and commercial libraries for linear programming. For a detailed list, see Linear Programming in Wikipedia or the Linear Programming Software Survey in OR/MS Today. In conclusion, we note that linear programming problems are still relevant today.

For each constraint in the primal problem, its associated dual price indicates how much the dual objective will change with a unit change in the right hand side of the constraint. In any solution to the dual, the values of the dual variables are known as the dual prices, also called shadow prices. Any feasible solution to D is an upper bound to P, and any feasible solution to P is a lower bound to D. Now, for the purpose of this blog post, imagine a situation where one is interested to create their watch list of the most popular TED talks given their constraints . We will see how to implement the Python program to help us create the watchlist in the optimal manner. Among optimization techniques, Linear Optimization using the Simplex Method is considered one of the most powerful ones and has been rated as one of the Top 10 algorithms of the 20th century.

Modify the assembly time constraint by changing its right-hand side by adding overtime. A hard constraint cannot be violated under any circumstances. So far, all constraints we have encountered are hard constraints. DOcplex helps you identify potential causes of infeasibilities, and it will also suggest changes to make the model feasible.

In summary, the maximum profit a company can make is $155.45 while producing 31.82 cups and 30 plates. Now we have the optimization problem formulated, we will need to solve it using gurobipy in Python. Linear programming is much easier to understand once we have an example of such an optimization problem. Karthikeyan Sankaran is currently a Director at LatentView Analytics which provides solutions at the intersection of Business, Technology & Math to business problems across a wide range of industries. Karthik has close to two decades of experience in the Information Technology industry having worked in multiple roles across the space of Data Management, Business Intelligence & Analytics. One way to solve it is to plot the equations on a graph, find the feasible area and then plug in the value of the vertices.

Python is an interpreted, interactive, object-oriented programming language. ChemPy is a Python library that provides functions and classes for solving chemistry related problems and collects parametrizations of chemical properties of substances from the literature. If you are interested in getting all optimal solutions you will need to find all optimal basis solutions as pointed you by @Erwin Kalvelagen here.

The values of the decision variables that minimizes the objective function while satisfying the constraints. The constraints on the raw materials A and B can be derived from conditions 3 and 4 by summing the raw material requirements for each product.

• Covering and packing LPs commonly arise as a linear programming relaxation of a combinatorial problem and are important in the study of approximation algorithms.
• Historically, ideas from linear programming have inspired many of the central concepts of optimization theory, such as duality, decomposition, and the importance of convexity and its generalizations.
• Understanding the theory behind linear programming, the simplex method, and each of the specific LP problems is really important.
• This work presents an integer linear programming formulation for solving the MPR problem when considering duplications, losses, and coalescence, and shows that the new algorithm is both accurate and scalable.

However, only PuLP has been mentioned as a Python library to formulating LP models. Step one convert the system of inequalities into matrix form. And we get the lowest cost of transportation of 16 thousand dollars.

Finally, the product amounts can’t be negative, so all decision variables must be greater than or equal to zero. Due to the transportation and storage constraints, the factory can consume up to one hundred units of the raw material A and ninety units of B per day. For each unit of the first product, three units of the raw material A are consumed.

This might help to better interpret the solution and help suggest which constraints may benefit from a change in bounds or a change into a soft constraint. You can determine which constraints are binding in a solution by examining the slack values with DOcplex. That is, changing the right hand side of the constraint will not affect the objective value.