Chapter 20 Numerical Differentiation

Content

• Section 4 1 Numerical Differentiation
• Project Details
• Applied Numerical Methods With Python For Engineers And

Another notable feature of the function is that it diverges to at . These unevaluated objects are useful for delaying the evaluation of the derivative, or for printing purposes. They are also used when SymPy does not know how to compute the derivative of an expression . This section covers how to do basic calculus tasks such as derivatives, integrals, limits, and series expansions in SymPy.

You can access it like any other library with import details. One topic many programming languages have difficulty with is symbolic mathematics. If you use Python though, you have access to the symbolic mathematics library Sympy. It is written entirely in Python, so you will not need to install any additional requirements. Next, we plot over the domain of interest, in this case from to 8.

In fact, all the finite-difference formulae are ill-conditioned and due to cancellation will produce a value of zero if h is small enough. If too large, the calculation of the slope of the secant line will be more accurately calculated, but the estimate of the slope of the tangent by using the secant could be worse. Redistributions of source code must retain the above copyright notice, this list of conditions and the following disclaimer. ‘Computing numerical derivatives for more general case is easy’ — I beg to differ, computing numerical derivatives for general cases is quite difficult. Symbolic differentiation is ideal if your problem is simple enough. SymPy is an excellent project for this that integrates well with NumPy. Look at the autowrap or lambdify functions or check out Jensen’s blogpost about a similar question.

Section 4 1 Numerical Differentiation

Here we will introduce only a few of these routines, the ones that are relatively simple and appropriate for the most common types of nonlinear equations. Theano is an open source numerical Python library that allows you to define, optimize, and evaluate mathematical expressions involving multi-dimensional arrays efficiently. My colleagues and I have decades of consulting experience helping companies solve complex problems involving data privacy, math, statistics, and computing. SciPy implements complex versions many special functions, but unfortunately not the zeta function. The right hand side formula $$ $$ can be implemented in python as long as we can compute the values $f(x+h/2)$ and $f(x-h/2)$. As $h to 0$, we should a good obtain approximation to $f’$. This function represents Tesla’s stock prices this year until yesterday .

Note that there are no explicit derivatives on the right hand side of the functions ; they are all functions of and the various , in this case and . Alternatively, check out our series of great free programming tutorials. The software can use GPUs and perform efficient symbolic differentiation.

It can also compute gradients of complex functions, e.g. multivariate functions. Just for the sake of completeness, you can also do differentiation by integration (see Cauchy’s integral formula), it is implemented e.g. in mpmath . Automatic derivatives are very cool, aren’t prone to numeric errors, but do require some additional libraries . This is the most robust but also the most sophisticated/difficult to set up choice.

Project Details

Therefore, here we are going to introduce the most common way to handle arrays in Python using the Numpy module. Numpy is probably the most fundamental numerical computing module in Python. The numdifftools package forPython was written by Per A. Brodtkorb based on the adaptive numerical differentiation toolbox written inMatlab by John D’Errico . Clearly the first member of this list is the domain of the symbolic toolbox SymPy, or some set of symbolic tools.

• Thus this is also a general method for obtaining high order differentiation rules.
• The Gamma and Error functions take one argument each and produce one output.
• Fortunately, many problems are much easier to solve if you use the derivative of a function, helping across different fields like economics, image processing, marketing analysis, etc.

In general, the eigenvalues can be complex, so their values are reported as complex numbers. Nevertheless, the FFT routines are able to handle data sets where is not a power of 2.

If you are not familiar with the math of any part of this section, you may safely skip it. At last, we can give the required value to x to calculate the derivative numerically. Efficient symbolic differentiation – derivatives for functions with one or many inputs. The following are 23 code examples for showing how to use numdifftools.Hessian().These examples are extracted from open source projects. You can vote up the ones you like or vote down the ones you don’t like, and go to the original project or source file by following the links above each example. A little rearrangement shows that the error in the one-sided difference, the first approximation above, is O. Now if you replace h with –h and do a little algebra you can also show that the two-sided difference is O.

Applied Numerical Methods With Python For Engineers And

Because the points are log spaced, the same rule applies at any scale, with only a scale factor applied. Numerical differentiation is based on the approximation of the function from which the derivative is taken by an interpolation polynomial. All basic formulas for numerical differentiation can be obtained using Newton’s first interpolation polynomial. For example, when finding the optimum of the values of functions.

It is implied in these formulas that the data points are equally spaced. If they are not evenly spaced, you need a different approach. An important consideration in practice when the function is calculated using floating-point arithmetic is the choice of step size, h. If chosen too small, the subtraction will yield a large rounding error.

Neither the name of the copyright holders nor the names of its contributors may be used to endorse or promote products derived from this software without specific prior written permission. Fixed issue #9 Backward differentiation method fails with additional parameters. Updated README.rst with info about how to install it using conda in an anaconda package. Refactored the taylor function into the Taylor class in order to simplify the code.

When I said “symbolic differentiation” I intended to imply that the process was handled by a computer. In principle 3 and 4 differ only by who does the work, the computer or the programmer. 3 is preferred over 4 due to consistency, scalability, and laziness. And if the step size is forced to be too small, then we see noise dominate the problem. The third class of differentiation problems is where Numdifftools is valuable.

Finite Differences

Finite differences require no external tools but are prone to numerical error and, if you’re in a multivariate situation, can take a while. However, if we force the step size to be artificially large, then approximation error takes over. The first row of gives the coefficients for 6’th order approximation. Looking at at row two and three, we see also that this gives the 6’th order approximation for the 3’rd and 5’th order derivatives as bonus. Thus this is also a general method for obtaining high order differentiation rules. As previously noted these formulas have the additional benefit of beeing applicable to any scale, with only a scale factor applied. Compute numerical derivatives of a function defined only by a sequence of data points.

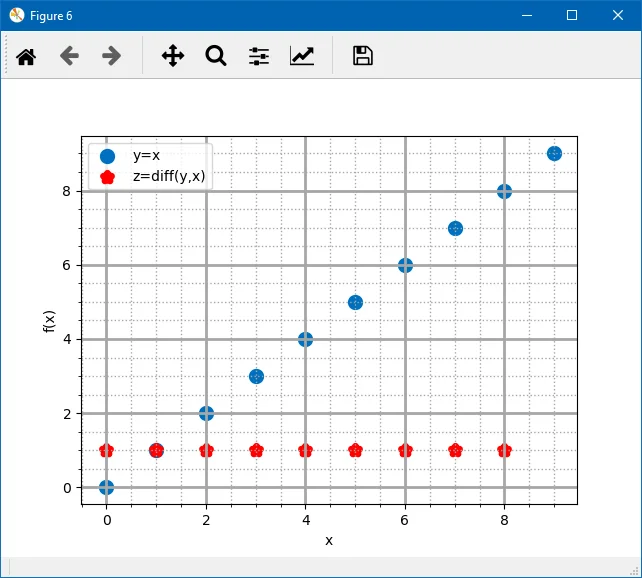
With C and similar languages, a directive that xph is a volatile variable will prevent this. This expression is Newton’s difference quotient (also known as a first-order divided difference).

Our introduction to these capabilities does not include extensive background on the numerical methods employed; that is a topic for another text. Here we simply introduce the SciPy routines for performing some of the more frequently required numerical tasks. Differential quadrature is the approximation of derivatives by using weighted sums of function values. Differential quadrature is of practical interest because its allows one to compute derivatives from noisy data. The name is in analogy with quadrature, meaning numerical integration, where weighted sums are used in methods such as Simpson’s method or the Trapezoidal rule. There are various methods for determining the weight coefficients, for example, the Savitzky-Golay filter. Differential quadrature is used to solve partial differential equations.